Proximo Seminario
De La Plata por el mundo
| Día | 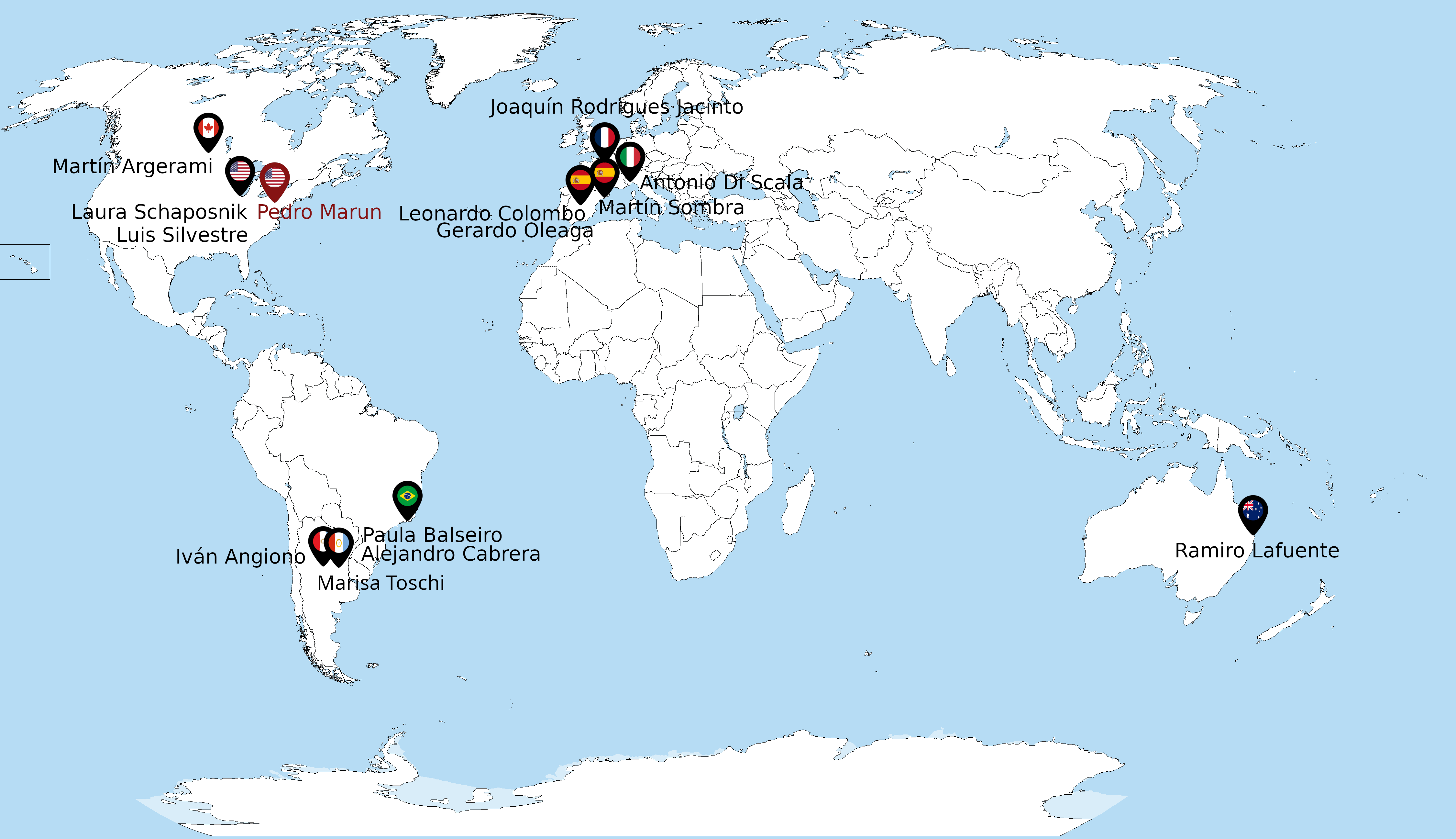TBA |  |
|
| Hora: | TBA | ||
| Lugar: | TBA | ||
| Expositor: | TBA | ||
| Título: |
TBA
|
||
| Resumen: | TBA | ||
De La Plata por el mundo
Durante el 2021 y comienzos del 2022 tendrá lugar el ciclo de charlas
"De La Plata por el mundo"
Las mismas estarán dictadas por matemáticas y matemáticos que se han graduado en la Universidad de La Plata y hoy se encuentran trabajando en distintos lugares del mundo.
Seminarios Previstos
Seminarios Anteriores
Seminarios 2021
Seminarios 2022
Contacto
Email: cmalp@mate.unlp.edu.ar
Tel/Fax: +54 221 4245875 / 4229476 / 4229850
Links
Departamento de Matemática
Facultad de Ciencias Exactas
Universidad Nacional de La Plata